Skip to contents

Gaussian Process regression

Source: vignettes/articles/standard-GP.Rmd
standard-GP.Rmd

Classical pipeline

The overall pipeline for standard GP regression in MagmaClustR can be decomposed in 3 main steps: training, prediction and plotting of results. The corresponding functions are:

Data

Dataset format

Before using train_gp(), our dataset should present a particular format. It must contains those 2 columns:

  • Input: numeric,
  • Output: numeric.

If we fail to ensure that the dataset satisfies those conditions, the algorithm will return an error.

The data frame can also provide as many covariates (i.e. additional columns) as desired, with no constraints on the column names (except the name ‘Reference’ that should always be avoided, as it is used inside internal functions of the algorithm). These covariates are treated as additional input dimensions.

Example with swimming data

To explore the features of standard GP in MagmaClustR, we use the swimmers dataset provided by the French Swimming Federation (available here, and studied more thoroughly here and there).

Our goal is to model the progression curves of swimmers in order to forecast their future performances. Thus, we randomly select a female swimmer from the dataset; let’s give her the fictive name Michaela for the sake of illustration.

The swimmers dataset contains 4 columns: ID, Age, Performance and Gender. Therefore, we first need to change the name and type of the columns, and remove Gender before using train_gp().

Michaela <- swimmers %>% filter(ID == 1718) %>% 
  select(-Gender) %>% 
  rename(Input = Age, Output = Performance)

We display Michaela’s performances according to her age to visualise her progression from raw data.

ggplot() +
  geom_point(data = Michaela,
       mapping = aes(x=Input,y=Output),
       size = 3,
       colour = "black") +
  theme_classic()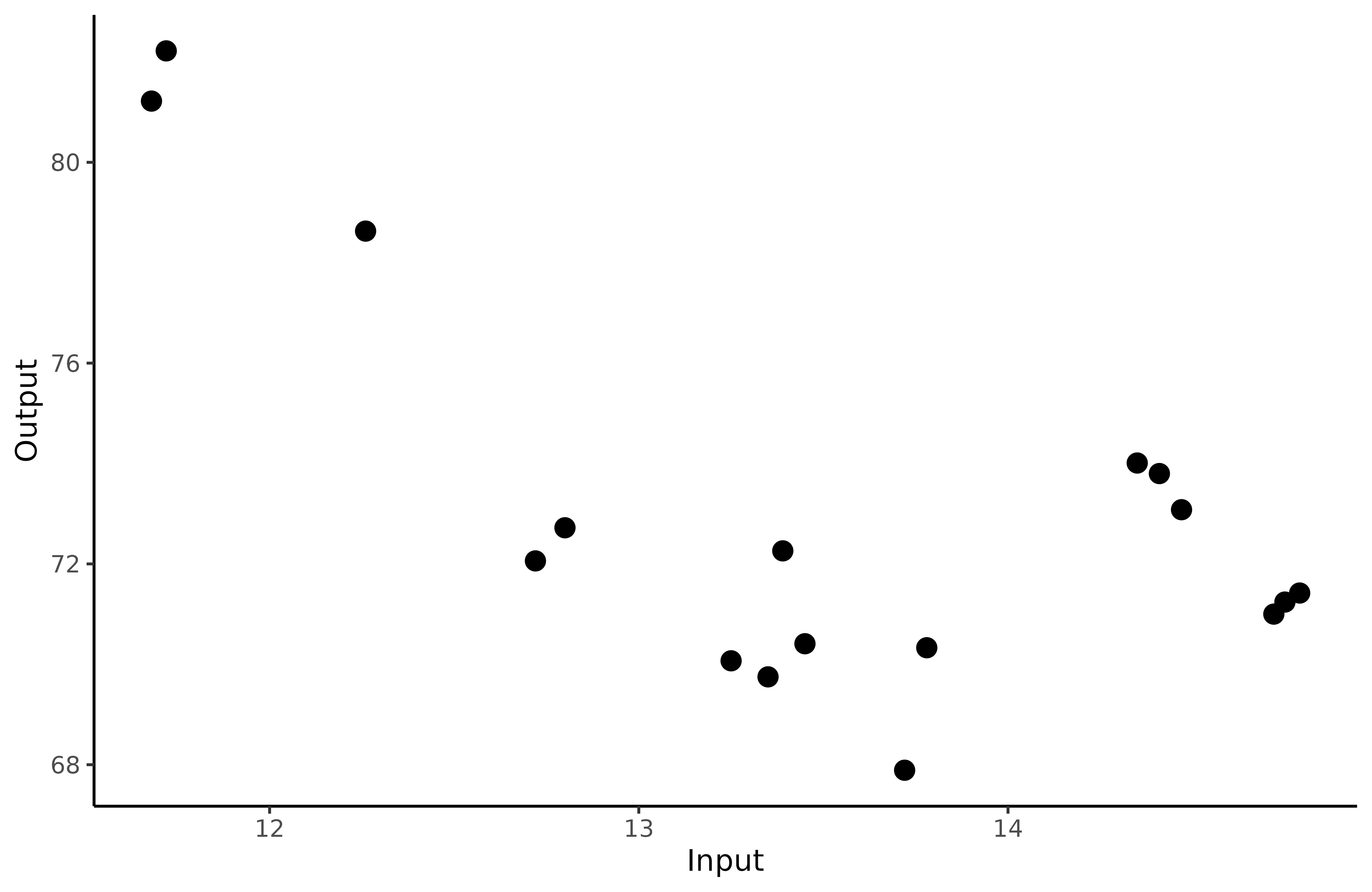

Fit a GP on Michaela’s data points

Training

To obtain a GP that best fits our data, we must specify some parameters:

  • prior_mean: if we assume no prior knowledge about the 100m freestyle, we can decide to leave the default value for this parameter (i.e. zero). However, if we want to take expert advice into account, we can modify the value of prior_mean accordingly.

  • kern: the relationship between observed data and prediction targets can be control through the covariance kernel. Therefore, in order to correctly fit our data, we need to choose a suitable covariance kernel. In the case of swimmers, we want a smooth progression curve for Michaela; therefore, we specify kern = "SE".

The most commonly used kernels and their properties are covered in the kernel cookbook. Details of available kernels and how to combine them in MagmaClustR are available in help(train_gp).

set.seed(2)
model_gp <- train_gp(data = Michaela,
                     kern = "SE",
                     prior_mean = 0)
#> The provided 'prior_mean' argument is of length 1. Thus, the hyper-posterior mean function has set to be constant everywhere. 
#>  
#> The 'ini_hp' argument has not been specified. Random values of hyper-parameters are used as initialisation.
#>

Thanks to train_gp(), we learn the model hyper-parameters from data, which can then be used to make prediction for Michaela’s performances.

GP prediction

The arguments kern and mean remain the same as above. We now need to specify:

  • the hyper-parameters obtained with train_gp() in hp;
  • the input values on which we want to evaluate our GP in grid_inputs. Here, we want to predict Michaela’s performances until 15/16 years old, so we set grid_inputs = seq(11, 15.5, 0.1).

See help(pred_gp) to get information about the other optional arguments.

pred_gp <- pred_gp(data = Michaela,
                   kern = "SE",
                   hp = model_gp,
                   grid_inputs = seq(11,15.5,0.1),
                   plot = FALSE) 
#> The 'mean' argument has not been specified. The  mean function is thus set to be 0 everywhere.
#>

Let us note that we could have called the pred_gp() function directly on data. If we didn’t use the train_gp() function beforehand, it is possible to omit the hp parameter; pred_gp() would automatically learn hyperparameters with default settings and us them to make predictions afterwards.

Plotting the results

Finally, we display Michaela’s prediction curve and its 95% associated credibility interval thanks to the plot_gp() function. If we want to get a prettier graphic, we could specify heatmap = TRUE to create a heatmap of probabilities instead (note that it could be longer to display when evaluating on fine grids).

plot_gp(pred_gp = pred_gp,
        data = Michaela)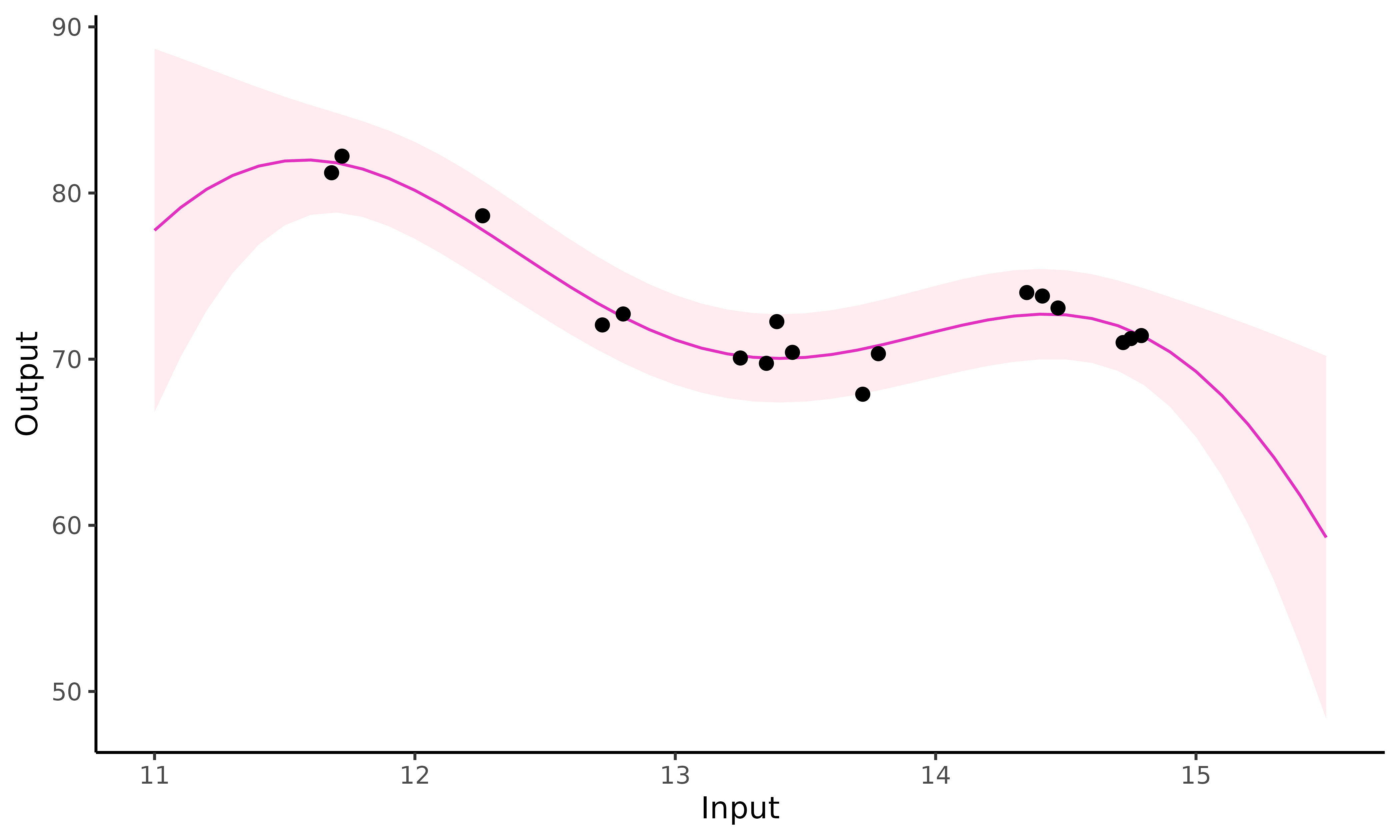

Close to Michaela’s observed data (\(t \in [ 10, 14 ]\)), the standard GP prediction behaves as expected: it accurately fits data points and the confidence interval is narrow. However, as soon as we move away from observed points, the GP drifts to the prior mean and uncertainty increases significantly.